XKCD Bad Map Projection with PostGIS
4 min readMore by this author
Last week, Randall Munroe dropped his latest XKCD "Bad Map Projection", number six, "ABS(Longitude)", which looks like this:
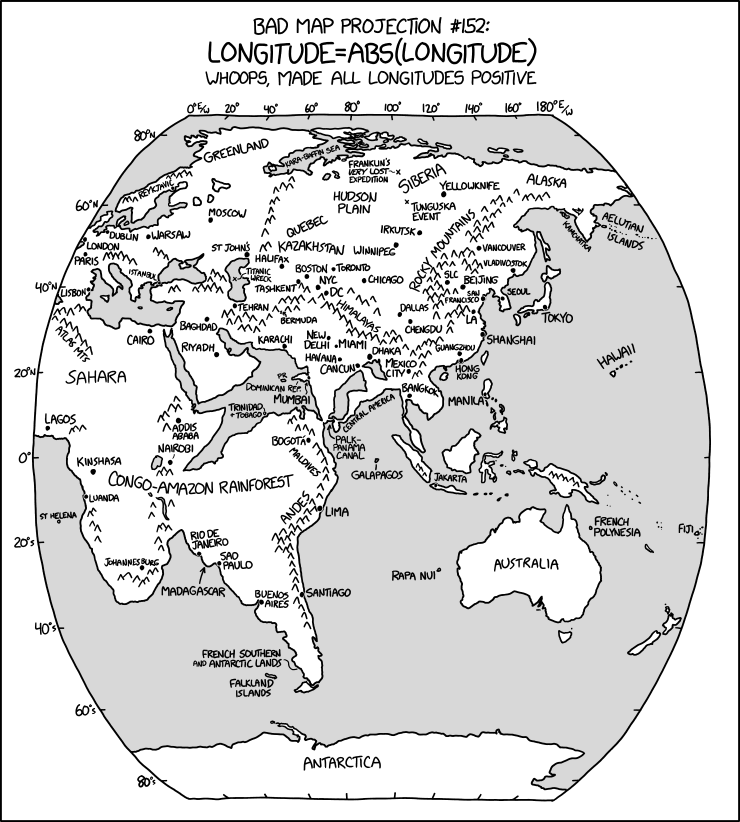
Truly this is a bad map projection, on a par with the previous five:
The last two are just applications of common map projections with very uncommon projection parameters that accentuate certain areas of the globe, a cartographic version of the classic "View of the World from 9th Avenue".

A colleague asked me if we could recreate ABS(Longitude) and I figured it was worth a try!
Getting Data
At a minimum, we want a countries layer and some independent place labels to provide context, which is available at the first stop for basic global data, Natural Earth.
We have been playing with ogr2ogr and weird remote access tricks lately, and we can use ogr2ogr to load the data in one step.
# Load the countries and places directly from the remote
# zip file into the working PostgreSQL database
ogr2ogr \
-f PostgreSQL \
-nlt PROMOTE_TO_MULTI \
-lco OVERWRITE=yes \
-lco GEOMETRY_NAME=geom \
postgresql://postgres@localhost/xkcd \
/vsizip//vsicurl/https://www.naturalearthdata.com/http//www.naturalearthdata.com/download/110m/cultural/ne_110m_admin_0_countries.zip
ogr2ogr \
-f PostgreSQL \
-lco OVERWRITE=yes \
-lco GEOMETRY_NAME=geom \
postgresql://postgres@localhost/xkcd \
/vsizip//vsicurl/https://www.naturalearthdata.com/http//www.naturalearthdata.com/download/110m/cultural/ne_110m_populated_places.zip
Preparing the Data
Now we have the data in the database, read to go!
The process we are going to apply will be transforming the shapes of one polygon at a time, and the Natural Earth data models the countries with one MultiPolygon per country.
Canada, for example, is one country, but 30 polygons.
We want a table with just one row for each polygon, so we "dump" all the multi-polygons using ST_Dump().
CREATE SEQUENCE country_id;
CREATE TABLE countries AS
SELECT nextval('country_id') AS id,
name,
(ST_Dump(geom)).geom::geometry(Polygon, 4326) AS geom
FROM ne_110m_admin_0_countries;
Next, because we are going to be processing western shapes with negative longitude different from eastern shapes we have to solve the problem: what to do with shapes that straddle the prime meridian?
The answer: ST_Split()!
First we create a prime meridian geometry to use as a "splitting blade".
CREATE TABLE lon_0 AS
SELECT ST_SetSrid(
ST_MakeLine(
ST_MakePoint(0,90),
ST_MakePoint(0,-90)),
4326)::geometry(LineString, 4326) AS geom;
Then we apply that blade to all the shapes that fall under it.
CREATE TABLE split_at_0 AS
SELECT id, name, ST_CollectionHomogenize(
ST_Split(c.geom, lon_0.geom))::geometry(MultiPolygon, 4326) AS geom
FROM countries c
JOIN lon_0
ON ST_Intersects(c.geom, lon_0.geom);
Surprisingly few countries end up chopped by the meridian.
The output of the split is, for each input polygon, a multi-polygon of the components. But we want to operate on the shapes one polygon at a time, so again, we must dump the multi-polygon into its components.
A slightly longer query dumps the split shapes, and stores them in a table with the rest of the un-split polygons, labeling each shape depending on whether it is "west" or "east" of the prime meridian.
CREATE TABLE countries_split AS
WITH split AS (
SELECT id, name, (ST_Dump(geom)).geom::geometry(Polygon, 4326) AS geom
FROM split_at_0
)
SELECT c.id, c.name, c.geom,
CASE WHEN ST_X(ST_StartPoint(c.geom)) >= 0 THEN 'east' ELSE 'west' END AS side
FROM countries c
LEFT JOIN split s
USING (id)
WHERE s.id IS NULL
UNION ALL
SELECT s.id, s.name, s.geom,
CASE WHEN ST_X(ST_StartPoint(s.geom)) >= 0 THEN 'east' ELSE 'west' END AS side
FROM split s;
We have divided the west from the east, and are ready for the final step.
Flipping the West
Now we are ready to apply a transformation to all the "west" countries, to turn their negative longitudes into positive ones.
To do this, we will use the powerful ST_Affine() function.
The two-dimensional form of the function looks like this:
ST_Affine(geom, a, b, d, e, xoff, yoff)
Where the parameters correspond to an affine transformation matrix:
Or, in equation form:
From the equation it is pretty clear, we want to negate the input x and leave everything else alone.
In order to get a pretty map, we'd like the output data to be centered on the prime meridian again, so:
And in SQL like this:
CREATE TABLE countries_affine AS
SELECT id, name,
CASE WHEN SIDE = 'west'
THEN ST_Affine(geom, -1, 0, 0, 1, -90, 0)
ELSE ST_Affine(geom, 1, 0, 0, 1, -90, 0)
END AS geom
FROM countries_split;
CREATE TABLE places_affine AS
SELECT ogc_fid AS id, name,
CASE WHEN ST_X(geom) < 0
THEN ST_Affine(geom, -1, 0, 0, 1, -90, 0)
ELSE ST_Affine(geom, 1, 0, 0, 1, -90, 0)
END AS geom
FROM ne_110m_populated_places
ORDER BY pop_max DESC;
And the final result on the map looks like the XKCD map, without the pretty hand-labeling and mountains:
The bad map projections aren't the only cartographic cartoons XKCD explored. If you liked this one, take a look at:
- Map Projections, all real!
- World According to Americans
- Upside Down
- Map Age Guide, fascinating history!